This article was originally published on September 25, 2010 at Pulsar Engine.
It has been updated to employ the conventions we use in Sauce instead of the ones I had previously used in Pulsar — aside from that, the content remains unchanged. This article still reflects my views and code.
Background
This post is related to the previous post on testing a return value that consists of a set of items with no predefined order (see Unit Testing Unordered Lists)[1]. However, it differs in that this time the problem is a little more mathematical in nature: how do we properly test a routine that performs an operation that may have multiple correct solutions?
For those of you who have written core math routines and solvers before, you know exactly what I’m referring to, but even if you haven’t I still encourage you to continue reading. I’ve chosen a relatively simple, common, yet important example to work through — there’s a good chance you’ll make use of this knowledge somewhere.
Unit Testing Ambiguity
There have been times when I’ve found myself trying to impose unrealistic expectations on my routines. Of course, when I test for them, I end up with failed tests and my first thought is more often than not: the code being tested must be wrong. However, the reality is that I have actually written a bad test.
A good example of this happened to me when I was working on my ComputeOrthoVectors() routine[2]. The purpose of the function is: given a single Vector3, compute two additional Vector3s which form an orthonormal basis with the input Vector3. So, I wrote the following test:
TEST(CanComputeOrthoBasisVectors)
{
Vector3 vecA;
Vector3 vecB;
ComputeOrthoBasisVectors(vecA, vecB, Vector3::UNIT_X);
CHECK_ARRAY_CLOSE(Vector3::UNIT_Y, vecA, 3, EPSILON);
CHECK_ARRAY_CLOSE(Vector3::UNIT_Z, vecB, 3, EPSILON);
}
The primary issue here is that the operation itself is soaked in ambiguity. More specifically, the two Vector3s that make up the return value can be produced by one of many valid solutions. To see this, let’s look at the math required for the implementation.
Computing an Orthonormal Basis
First, let’s be clear on the terminology: a set of three Vector3s that are each perpendicular to the other two is called an orthogonal basis. If we normalize the vectors in the set, we can call it an orthonormal basis. In other words: A 3D orthonormal basis is a set of three vectors that are each perpendicular to the other two and each of unit length.
The need for creating an orthonormal basis from a single vector is a fairly common operation (probably the most common usage is in constructing a camera matrix given a “look-at” vector).
Given two non-coincident[3] vectors, we can use the cross product to find a third vector that is perpendicular to both the input vectors. This is often why we say that two non-coincident vectors span a plane, because it is from these two vectors that we can compute the normal to that plane.
The thing to note here is that there are an infinite number of valid non-coincident vectors that span a plane. You can imagine grabbing the normal vector as if it were a rod connected to two other rods (the input vectors) and spinning it; any orientation you spin it to is a valid configuration that would produce the same normal vector. I have created an animation demonstrating this below:
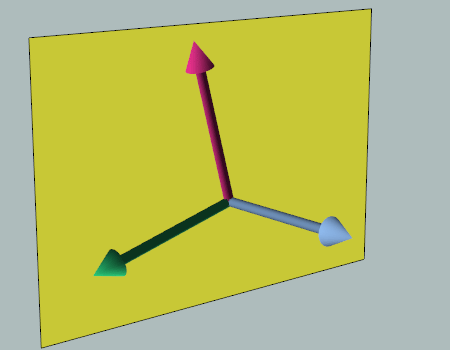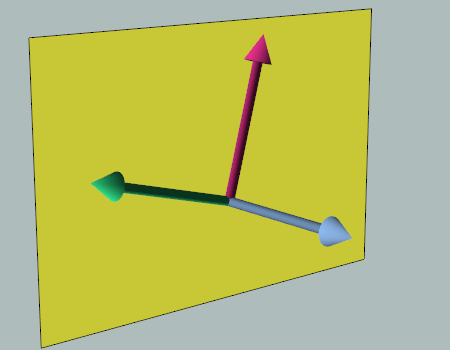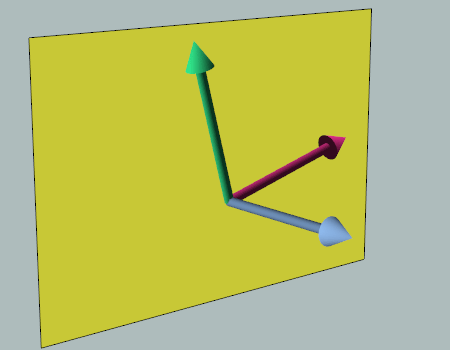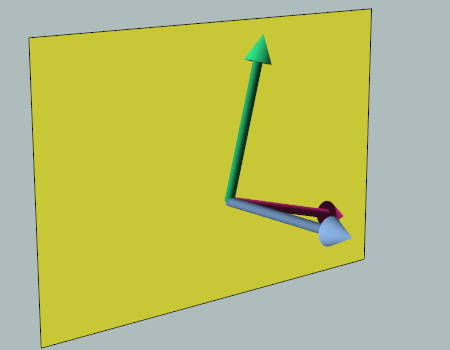
In essence, this is why the results of the operation are valid, yet, for the lack of a better word, ambiguous. In the case of our routine, we are supplying the normal and computing two other vectors that span the plane. The fact that the two returned vectors are orthogonal to the input vector does not change the fact that there are an infinite number of configurations.
Testing the Geometry, Not the Values
Returning to the original testing dilemma, since there are an infinite number of possible solutions for our returned pair of Vector3s, if we write tests that check the values of those vectors, then our tests will be bound to the implementation. The result is a ticking time-bomb that may explode in our face later on (maybe during an optimization pass) because, although we may change the pair of vectors returned for a given input, the three vectors still form an orthonormal basis — the correct and desired result — in spite of the fact that we now have failing tests.
My solution was to check the following geometric properties:
- All three vectors are perpendicular to each other (in other words, they form an orthogonal basis).
- The two returned vectors are of unit length (input vector is assumed to be normalized).
The following are a few tests (straight from my codebase) that employ this approach:
TEST(CanComputeOrthoBasisVectors_UnitX)
{
Vector3 vecA;
Vector3 vecB;
ComputeOrthoBasisVectors(vecA, vecB, Vector3::UNIT_X);
CHECK_CLOSE(0.0f, vecA.Dot(vecB), EPSILON);
CHECK_CLOSE(0.0f, vecA.Dot(Vector3::UNIT_X), EPSILON);
CHECK_CLOSE(0.0f, vecB.Dot(Vector3::UNIT_X), EPSILON);
CHECK_CLOSE(1.0f, vecA.Mag(), EPSILON);
CHECK_CLOSE(1.0f, vecB.Mag(), EPSILON);
}
TEST(CanComputeOrthoBasisVectors_UnitY)
{
Vector3 vecA;
Vector3 vecB;
ComputeOrthoBasisVectors(vecA, vecB, Vector3::UNIT_Y);
CHECK_CLOSE(0.0f, vecA.Dot(vecB), EPSILON);
CHECK_CLOSE(0.0f, vecA.Dot(Vector3::UNIT_Y), EPSILON);
CHECK_CLOSE(0.0f, vecB.Dot(Vector3::UNIT_Y), EPSILON);
CHECK_CLOSE(1.0f, vecA.Mag(), EPSILON);
CHECK_CLOSE(1.0f, vecB.Mag(), EPSILON);
}
TEST(CanComputeOrthoBasisVectors_UnitZ)
{
Vector3 vecA;
Vector3 vecB;
ComputeOrthoBasisVectors(vecA, vecB, Vector3::UNIT_Z);
CHECK_CLOSE(0.0f, vecA.Dot(vecB), EPSILON);
CHECK_CLOSE(0.0f, vecA.Dot(Vector3::UNIT_Z), EPSILON);
CHECK_CLOSE(0.0f, vecB.Dot(Vector3::UNIT_Z), EPSILON);
CHECK_CLOSE(1.0f, vecA.Mag(), EPSILON);
CHECK_CLOSE(1.0f, vecB.Mag(), EPSILON);
}
TEST(CanComputeOrthoBasisVectors_RefPaperExample)
{
Vector3 vecA;
Vector3 vecB;
const Vector3 unitAxis(-0.285714f, 0.857143f, 0.428571f);
ComputeOrthoBasisVectors(vecA, vecB, unitAxis);
CHECK_CLOSE(0.0f, vecA.Dot(vecB), EPSILON);
CHECK_CLOSE(0.0f, vecA.Dot(unitAxis), EPSILON);
CHECK_CLOSE(0.0f, vecB.Dot(unitAxis), EPSILON);
CHECK_CLOSE(1.0f, vecA.Mag(), EPSILON);
CHECK_CLOSE(1.0f, vecB.Mag(), EPSILON);
}
By testing these properties, as opposed to testing for the resulting vector values directly (as in the original test shown above), it doesn’t matter how the internals of the ComputeOrthoBasisVectors() produces the two returned Vector3s. As long as the input vector and the returned vectors all form an orthonormal basis, our tests will pass.
Final Thoughts
My hope is that the example presented in this article demonstrates one of the pitfalls of having tests that depend on the internal implementation of the routine being tested. As I have stated before, although it is important to write tests for the functionality, it can be difficult to recognize when a test is bound to the implementation.
A good place to start looking for this sort of scenario is in tests that explicitly check return values. Certainly, explicit checks is actually what you want in most cases, but for some operations it is not.
Footnotes
- Originally, these two topics were going to be addressed in a single article, but I decided against it in hopes that keeping them separate would allow for more clarity in each.
- In fact, the trouble I had in testing the
ComputeOrthoVectors()routine is what inspired me to post both this article and the last. - Two vectors are said to be coincident if they have the same direction when you discard their magnitudes. In other words, two vectors are coincident if you normalize both of them and the results are the same.
References
- Möller, Tomas and John F. Hughes. Building an Orthonormal Basis from a Unit Vector. [ pdf ]